
Mathematical Concepts in Orientation (15 months – 3 years old)
Maria Montessori believed that toddlers learn mathematical concepts through everyday practical life experiences, such as caring for themselves, the environment, and others. Sweeping and other practical life skills allow the child to develop concepts such as order, problem-solving, cause-and-effect, concentration, and critical thinking. We provide opportunities daily for the child to engage in such hands-on, concrete activities, which in turn lead to independence, confidence, self-regulation skills. When children have developed good self-regulation skills, they can invest more in their learning.
Order. At this stage, Orientation children are trying to make sense of their world and their place in the world. One of the first activities to develop an internal sense of order is isolating a single variable, such as color. In a sorting exercise, a child receives items of the same shape and size but of different colors. The child also receives a single bowl with a single color on the outside of that bowl. The child then selects the item of the same color and places that item in the bowl. Through holding, seeing, sorting, and classifying the object, the child develops an understanding of order and correlation.

Quantity and Sequencing. Teachers in Orientation introduce and reinforce quantity and sequencing by speaking about everyday events. For example, at snack time, the teacher will ask the student, “I see your plate is empty. Would you like more? How many strawberries would you like? Would you like one strawberry [teacher places strawberry on plate] or two strawberries [teacher places another strawberry on plate]?” By pointing to the objects, counting with them, and involving students, the teacher collaborates with the student and builds on the student’s natural desire to learn and absorb information. Teachers also use language purposefully to teach about sequencing and order. For example, a teacher may guide a student to, “First, put on your sock. Second, put your shoe on.” Or, to minimize spills at lunchtime cleanup, a teacher may advise a student, “First, take your plate. Second, get your water bottle. Third, get your lunchbox.” Through mindful communication, the student is invited and allowed to take everything in and actively participate in the lesson.
One-to-One Correspondence. Children in Orientation engage in counting from memorization or rote counting, which helps the children develop order and sequencing. The exercise is meaningful because it helps children learn quantities, numbers, and the relationships between them. However, the child may not understand one-to-one correspondence–the notion that “one” means the quantity of 1, that each number corresponds to a discrete unit. In a lesson for older Orientation students, the teacher will present a card bearing a unit (for example, an apple) and counters (for example, plastic apples). If the card bears one apple, the child will place one apple counter on that card. If the card bears two apples, the child will place two apples on that card, and so on. In doing so, the child learns that “one” and “two” are not just words; one is a unit of 1; two is a quantity of 2.

Numeric Symbols. Once a child has a good foundation of sorting, one-to-one correspondence, rote counting, and the basis for understanding quantity, the teacher will introduce a more abstract concept, matching symbols with quantity. In a sample exercise, the child will be asked to match a card bearing the number 1 with a card displaying 1 object; a card bearing the number 2 with a card displaying 2 objects; a card bearing the number 3 with a card displaying 3 objects, and so forth. In this manner and over time, the child is prepared for math in the Primary level.

Math in Primary (3 – 6 years old)
When a child enters the Primary program, teachers may engage the child in simple exercises to determine the child’s mastery of mathematical concepts. For example, a parent may tell the teacher that his child can count to 50. To explore the child’s understanding of one-to-one correspondence, the teacher will carefully place 5 objects in a row. The teacher will ask the child, “How many objects are there?” The teacher will then randomly drop the 5 objects. The child is asked again, “How many objects are there?” If the child does not know, the teacher will begin to work with the child on one-to-one correspondence. In this manner, the transition from Orientation to Primary is seamless.
One-to-One Correspondence and Numeration. The teacher will present visual representations of quantity — 1 dollar matched with 1 envelope — to reinforce the concept that “one” means the quantity of 1, that each number corresponds to a discrete unit. In addition, the teacher may introduce the child to sandpaper numbers, ten green boards displaying the numbers 0-9. The numbers are distinguished from the smooth green background in that they are cut out of fine-grit sandpaper, inviting the child to touch the different textures of the numbers. The teacher may present the sandpaper number bearing the number 1 and remind the child, “Remember, this is one?”
The red and blue rods are intentionally beautiful when on display in the classroom, inviting the child to explore and work with the material. The differing sizes of the rods and purposefully counting the alternating colors of the rods help the child internalize how quantities move from very small to very big.
In a first exercise, the child will move the rods and cards bearing the numbers 1-10 to her mat, the working area of the Montessori child. The teacher will count the colored sections of each rod, asking the child questions such as, “1. Can you find the number 1? 1, 2. Can you find the number 2?” The child will place the card next to the rod bearing the same number of colored sections. To reinforce the concept of, for example, the number 3, the teacher will ask, “Can you point to [the card bearing the number] 3? Can you count [the colored sections of the rod] to 3? What number is this [while pointing to the number 3]?” The child demonstrates her mastery of the concept by taking in new information, passive recall, and active identification.
The child and the teacher will move sequentially through the rods, never skipping the steps of counting the colored sections and then placing the card bearing the same number next to the rod. The child will repeat this lesson several times a day for several consecutive workdays. The teacher, observing the child and checking for understanding, may ultimately ask the child to teach the lesson to another child.
Math Operations. Using the same red and blue rods, the teacher will engage the child as follows, “These are the same rods. I wonder what would happen if I put 2 and 3 together.” Using “put together” instead of “add together” allows the child to feel confident in her ability to add by “putting together” two rods. The child then counts the colored sections of the two rods, counting 1, 2, 3, 4, 5. The child checks her work using the rod with 5 colored sections, the “checker.” Using the “checker,” the child sees that she does not need the teacher, that she can check her work herself. The child continues to work through various number combinations and checking the number combinations.

Seeing that the child can accomplish simple addition, the teacher will take the child on a journey “in search of the number 10.” The teacher will introduce the smallest rod (1 colored section) and the biggest rod to the child (10 colored sections). The teacher will ask the child, “How many does the biggest rod have?” To which the child will answer, “10.” The teacher will continue, “I wonder what makes 10.” The child will select a rod, for example, a rod with 7 colored sections. The teacher will ask, “What else do we need to make 10?” The child may then select a rod with 3 colored sections. The child counts the colored sections of the two rods, counting 1, 2, 3, 4, 5, 6, 7, 8 , 9, 10, and checks the answer using the rod with 10 colored sections.

The large tactile surfaces of the red and blue rods give way to delicate bead groupings, purposefully ordered in two series and used to learn place value and operations in Primary and beyond. The Primary student will use the bead stairs to learn skip counting and other math operations. The bead stairs consist of strands of colored beads as follows: 1 red bead; 2 green beads; 3 pink beads; 4 yellow beads; 5 light blue beads; 6 purple beads; 7 white beads; 8 brown beads; 9 dark blue beads. The Primary student will use the golden beads to master place value and what it means for a number to consist of units, tens, hundreds, and thousands. The golden beads series is comprised of golden beads as follows: 1 bead; 10 beads in a strand; 100 beads in a square; 1,000 beads in a cube.
Primary Math Skills. Using the Socratic method to develop critical thinking and Montessori materials to allow the child to wrap her hands and mind around math concepts, a Primary student (3 – 6 years old) typically learns:
- Numeration (0-9,999);
- Addition (up to 4-digit numbers);
- Subtraction (up to 4-digit numbers);
- Skip counting (up to 1,000) and multiplication concepts; and
- Geometric shapes.
Math in Lower Elementary (1st – 3rd grade)
The student enters Lower Elementary with a strong foundation of fundamental math and math concepts. The Lower Elementary teacher meets the student where he is and builds on that knowledge, introducing nomenclature applicable to math operations.
- Addition
- addend + addend = sum
- Subtraction
- minuend – subtrahend = difference
- Multiplication
- factor x factor = product
- multiplicand x multiplier = product
- Division
- dividend ÷ divisor = quotient [remainder]
The student may practice these concepts using math cards, which contain the math problem depicted in numbers on the front and in words on the back. The cards are progressive and allow the student to move forward and backward, seamlessly and at the student’s own pace, to learn, check, and reinforce mathematical concepts.
Introducing Division. The student will begin the lesson by preparing his mat. On his mat, he will place a card bearing a math problem — e.g., 4,864 ÷ 2 — paper, pencil, and the stamp game. The student is familiar with the stamp game as he has used it to learn addition, subtraction, and multiplication. The stamp game contains tiles purposefully colored in a scheme introduced in the student’s years in Primary.
The student will begin by writing the problem — e.g., 4,864 ÷ 2 — on paper. The lesson may then proceed as follows, as narrated by the teacher.
“Today, we are going to learn about a new operation, which is division. Here’s the tricky thing — in division, you begin in the highest place value. This is different from addition, subtraction, and multiplication, where you start at the units place. But in division, we start in the highest place value. Maybe today, the highest place value is hundreds, and maybe later, the highest place value is trillions. You never know.”
“A long time ago, there was a group of friends, and they were green. They all did the same amount of work, and they were all paid the same amount of money. When we were doing division, we will pass out [tiles] to our friends, starting with tiles of the highest place value.”
The teacher may pause here to review the vocabulary associated with addition, subtraction, and multiplication. In this manner, the teacher checks for understanding before moving on.
At this time, the student has placed the following on his mat.
- 2 green pegs (the 2 friends)
- 4 green tiles bearing the number 1,000
- 8 red tiles bearing the number 100
- 6 blue tiles bearing the number 10
- 4 green tiles bearing the number 1
“Now, starting at the highest place value, we have four 1,000 tiles, and we’re sharing them between two friends. The rule is that if we give one to a friend, we give one to the other friend because division is sharing equally. One 1,000 to a friend; one 1,000 to the other friend; one 1,000 to a friend; one 1,000 to the other friend. Do you think we can keep going? We have already given out our 1,000s; what’s the next highest place value? Let’s move on to the 100s.”
The student will proceed to distribute the tiles equally amongst the two friends.
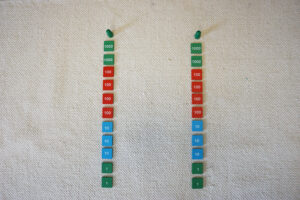
“The answer to a division problem is called a quotient. The answer to a division problem is how much one friend / one unit receives. So, it doesn’t matter how many tiles you have put out in total; we only care about one unit. How many thousands did this one unit receive? [2,000] How many hundreds? [400] How many tens? [30] How many ones? [2] And so the answer to our division problem, 4,864 ÷ 2 is 2,432.”
The student will write down the answer, and the teacher will check it. Progressing through the math cards, the teacher will reiterate that the answer (the quotient) is what one unit receives and that the student should always start with the highest place value. The difficulty will increase, including odd numbers and exchanging as in one 10 can equal 10 units, two-digit divisors and three-digit divisors, and long division by third grade. As the student progresses to group division and long division, tiles in the stamp game are replaced with beads in the test tubes work, a material that will be used again in Upper Elementary.
Lower Elementary Math Skills. Leveraging math materials, parameters, and rationales, the student gains a deeper understanding of the why and how behind math facts. Often, a student will realize that the materials are no longer necessary, and the student will want to solve the problem on paper alone, moving towards abstraction. Eventually, the materials are put away, and the student relies on his intrinsic knowledge of math facts. The math journey of a Lower Elementary student (1st – 3rd grade) normally includes the following topics.
- Positive and negative numbers
- Fractions and decimals, as also applied to telling time and money
- Addition
- Subtraction
- Multiplication
- Division
- Measurement and graphing
- Geometric shapes
Math in Upper Elementary (4th – 6th grade)
Upper Elementary builds on the mathematical nomenclature and knowledge attained in Lower Elementary, adding vocabulary describing exponents and radicals as well as 2D and 3D geometric shapes and equations. The study of geometry sparks the student’s interest in their world and interest in learning to measure their world. Each lesson builds on previous skills.
The Upper El geometry curriculum challenges students to handle, manipulate, and judge the relationships between geometric figures. Through this student-centered, inquiry-driven approach to geometry, students hone their logical and creative functions. This approach also promotes flexible thinking as students discover multiple ways to prove and disprove geometric hypotheses. Complex ideas are presented in a concrete manner, allowing students to develop deductive logic and gain access to geometric concepts usually presented in much later grades.
Geometry is the art of mathematics. Geometry, through art, reveals a different side of math and has the capacity to reach a student that may not naturally be led to the study of mathematics. In the Montessori classroom, students are expected to explain their thinking in pictures as well as through words. Precision, just as in science and math, is essential as we work to understand the geometric world around us. We are, after all, surrounded by the beauty of geometry in the nature we witness every day.
Exploring Geometry. Demonstrating the continued use of the Socratic method, below are questions that an Upper Elementary teacher may ask as the student explores the area of a triangle.
- Let’s review the nomenclature of the triangle. What is base? What is height? What is altitude? What is hypotenuse? What are angles?
- Cut the equilateral triangle at the midpoint of the altitude (height). What shapes have been formed?
- Cut the small equilateral triangle into two pieces along the altitude. What is a right angle? What is scalene? What is equilateral? What is the hypotenuse?
- Rotate and dock each of the right-angled scalene triangles to each hypotenuse. How would we develop a formula for calculating the area of a triangle? What is the formula? [Area = (height x base) / 2] Through this inquiry-based lesson, the student will visualize the components of the area of a triangle and derive the formula.

Upper Elementary Math Skills. Montessori math materials play a supportive role in Upper Elementary, allowing the student to move to greater levels of complexity and abstraction with confidence. The math journey of an Upper Elementary student (4th – 6th grade) is student-centered and student-paced and usually includes the following topics.
- Math operations (addition, subtraction, multiplication, division) with:
- Whole numbers
- Fractions
- Mixed numbers
- Decimal numbers
- Negative numbers
- Roots/radicals and exponents
- Geometry (typical scope and sequence)
- Conservation of area: congruency, similarity, and equivalency (CSE)
- Triangle boxes (continued study of CSE)
- Hexagonal boxes (continued study of CSE)
- Constructions: lines, segments, angles
- Attribute blocks and classification
- Area: various quadrilaterals
- Circles
- Constructions: bisecting and perpendicular lines; angles
- Pythagorean theorem
- Classification of solids
- Tessellations
- Attribute blocks
- Volume: prisms, pyramids, cylinders, cones, spheres
- Surface area: cones, cylinders, spheres
- Middle Years math, based on the aptitudes of the student
Middle Years Math Curriculum (7th and 8th grade)
The Montessori Middle Years math curriculum is designed to develop and fortify students’ understanding of abstract math. At this stage of the mathematics journey, we focus on fluency in mathematical concepts by emphasizing literacy, verbal expression, and written language. The rhythm of the class mirrors the Montessori three-period lesson (introduction, recognition, and recall). Students are provided a brief introduction to a mathematical concept in the first period lesson. In the second period, they are given the opportunity to explore the various iterations of the mathematical concept. In the third period, their knowledge is formally assessed and documented.
Students are assessed and placed in the appropriate course, with curriculum pacing that matches the aptitudes of the student. In the Montessori Middle Years program, we offer a range of math courses:
- Math 7
- Pre-Algebra
- Algebra (eligible for high school credit)
- Geometry (eligible for high school credit)
